Universal corrections to the Kibble-Zurek scaling law across imperfect critical points
Continuous phase transitions are ubiquitous in nature and are marked by the appearance of critical points separating distinct phases of matter. Near these points, the dynamics are governed by the spontaneous breaking of a continuous symmetry, driving the system from a disordered to an ordered state. Remarkably, the physics in the vicinity of a critical point is largely universal: a small set of numbers—the critical exponents—controls almost all relevant behavior near the transition.
This universality extends beyond equilibrium. It also governs out-of-equilibrium processes such as rapid parameter changes, commonly referred to as quenches, that drive a system across a critical point. As independently recognized by Kibble and Zurek, crossing a critical point at a finite rate inevitably leads to the formation of topological defects, whose density follows a universal scaling law determined by the quench rate and the same critical exponents. This phenomenon, known as the Kibble–Zurek mechanism, has been experimentally confirmed in a wide range of classical and quantum systems.

Figure 1: An external symmetry breaking parameter modifies a sharp 2nd order phase transition (blue line) into a smooth crossover or imperfect phase transition (green profile). The setup consists in quenching the system from an initial state near the original critical point (T=Tc) deep into the ordered phase (T=Tf). The right cartoon highlights the creation of topological defects (vortices) by jumping across this imperfect critical point.
Despite the success of this paradigm, many phase transitions and critical points in nature are imperfect. In these cases, the symmetry that would be spontaneously broken at criticality is already only approximate. Well-known examples include chiral symmetry in QCD and charge-density-wave transitions in metals with impurities.
What happens, then, when a system is driven across such an imperfect critical point, as illustrated in Fig. 1? How does the number of defects formed depend on the quench rate? And, crucially, do the Kibble–Zurek predictions survive, or do they break down?
In a recent publication, a team led by Matteo Baggioli (SJTU Shanghai), in collaboration with Hua Bi Zheng (Hainan University), Sebastian Grieninger (Stony Brook), Chaun-Yin Xia (Hainan University), and Peng Yang (SJTU Shanghai), demonstrated the emergence of a universal exponential correction to the Kibble–Zurek scaling law (see Fig. 2). This correction arises when the transition is a crossover associated with an approximate symmetry, rather than a perfect critical point. This universal form has been demonstrated using both weakly-coupled models (Ginzburg Landau formalism) but also strongly coupled modes constructed using the holographic duality.
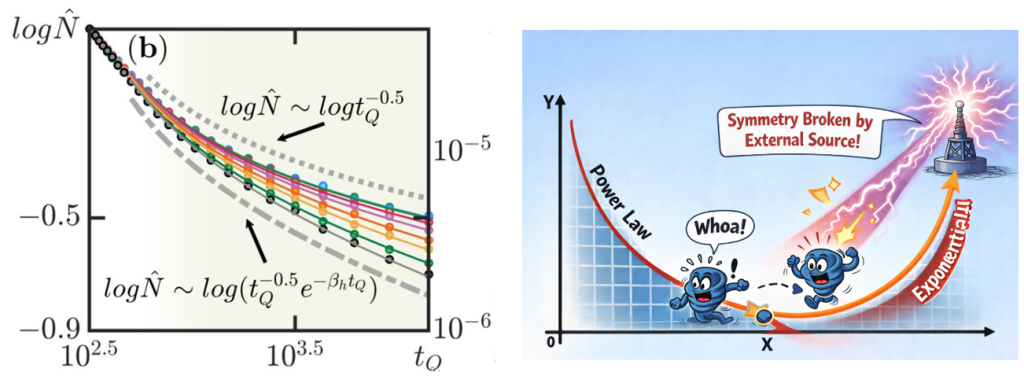
Figure 2. The universal exponential correction discovered by Baggioli, Yang and collaborators. The number of topological defects created during the quench does not follow anymore the Kibble Zurek universal scaling law but presents a new exponential correction that depends universally on the external field breaking explicitly the symmetry.
This discovery reveals that the universal physics of critical points and phase transitions can persist even in the presence of imperfections or explicit symmetry-breaking terms. The newly identified correction is expected to be observable in future experiments and to arise in a wide range of physical systems.
The findings are published in Physical Review Letters, Phys. Rev. Lett. 136, 051602 (2026)
