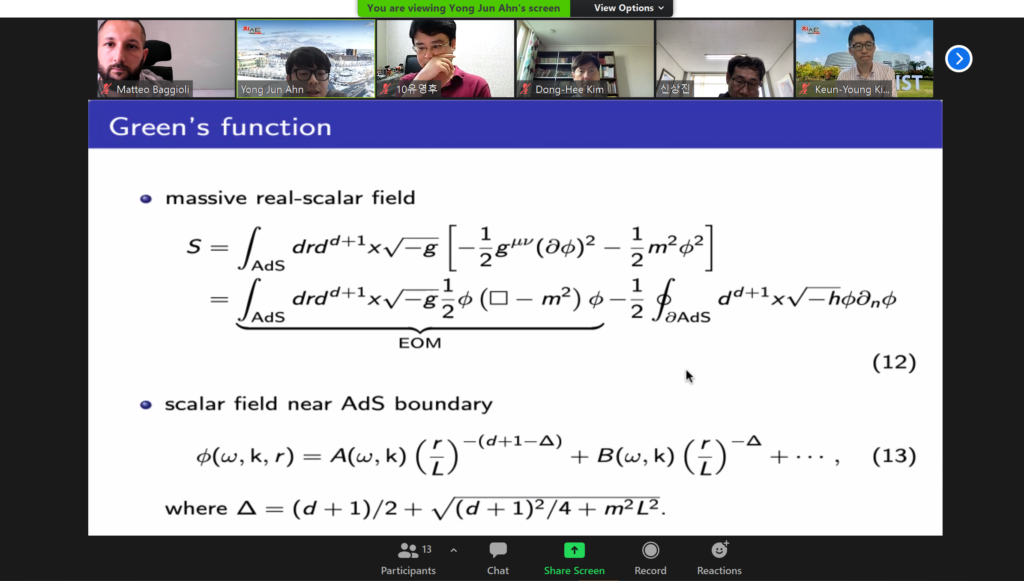
Yong Jun defended his PhD thesis today!


Matteo attended and presented his recent work in the “GRA 2020/2021 Annual Conference and National Congress on Gravity” in Shenyang, China (23-26 April 2021).


Our future PhD student Giorgio Frangi just defended his master thesis under the supervision of Matteo, Prof. Alessio Zaccone and Prof. Oriol Pujolas. He obtained the maximum grade and he is ready for his next step!
Congratulations Giorgio !!!
And thanks to Alessio and Oriol for supporting TheoryLab!
Matteo attended and presented at the “2021 International Workshop on Soft Matter and Biophysics Theories—Youth Forum”, which was organized by the Institute of Theoretical Physics, Chinese Academy of Sciences (ITP-CAS) and CAS Key Laboratory for Theoretical Physics, and hosted by Minjiang University.
Minjiang University, Fuzhou, Fujian, March 22nd– 25th 2021

In an article published in the journal PNAS by Matteo Baggioli, and Alessio Zaccone of University of Milano, the law which governs the distribution of vibrational energy states of liquids has been derived mathematically for the first time. The new mathematical theory by Zaccone & Baggioli solved the problem of obtaining the distribution of these complex energy states by combining the so-called Zeldovich regularization for unstable quantum states with the mathematical theory of distributions by L. Schwartz. The final result provides an equation in closed form for the distribution of energy states in liquids, which goes linear in the frequency, as opposed to the Debye law for solids, which goes quadratic in frequency, and also correctly predicts its temperature dependence.
Universal law for the vibrational density of states of liquids | PNAS

The team is growing! From September 2021 we will have 3 new members: Takaaki Ishii, Yongjun Ahn and Giorgio Frangi. Welcome to Shanghai !


